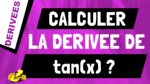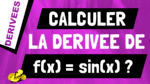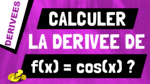Dans cette vidéo, on va voir comment tu peux calculer la dérivée de la fonction k*f(x).
L’erreur à ne pas faire…
Alors ça c’est très important parce que je vois trop d’erreurs sur cette chose là dans les cours que je donne avec mes élèves. Beaucoup d’élèves vont vouloir faire comme si k c’était une fonction !
C’est-à-dire qu’ils vont dériver ça sous la forme u * v, et ils vont oublier qu’en fait, c’est juste un réel ici. k, il appartient aux réels. C’est hyper important ici !
La dérivée de k*f(x)
Il est important de savoir que k * x, la dérivée k * f(x), quand tu multiplies une fonction par un réel, sa dérivée est multipliée par le même réel. Donc ça c’est simplement k * f'(x).
C’est vraiment tout simple, mais c’est hyper important, il ne faut pas que tu oublies ça, parce que si tu commences à te compliquer la vie avec du u * v, tu vas pas t’en sortir. Même si ça fonctionne évidement.
C’est utile pour les primitives.
Je vais le faire juste après, mais c’est beaucoup plus compliqué. Et ça, ça va être hyper utile au moment où tu fais tes primitives, parce que quand tu vas chercher les primitives et que t’as pas le bon facteur devant.
Eh bien, qu’est ce que tu vas utiliser ? Tu vas utiliser le fait que k fois la primitive, ça va te donner k fois la dérivée. Ce qui est important ici c’est ça !
Des exemples.
Donc, je vais prendre des exemples ici, si tu as 18 * x^2, eh bien la primitive de 18 * x^2 c’est 18 fois la primitive de x^2. Et donc ça c’est bien 18 * 2x. Donc c’est 36x.
C’est important parce que c’est ça, tu connais toutes les primitives usuelles, x^2, x^n, ln(x), 1/x, etc. Donc, à partir du moment où tu peux l’écrire sous la forme un réel fois une fonction que tu connais, tu sais dériver, eh bien tu peux tout simplifier sous cette forme là.
Par exemple avec racine de x, si t’as 4 √x à dériver. Eh bien tu sais dériver racine de x. Donc (4 √x)’ = 4 *(√x)’. La dérivée de √x c’est 1/2√x. Donc ici tu vas avoir 4 * (1/2√x). Donc ça, ça va te donner 2/√x.
L’important c’est de tout ramener à la dérivée usuelle. Alors juste pour le fun parce que je sais qu’il y en a qui aiment bien faire ça, se compliquer la vie.
La version compliquée…
Ici tu peux dire, eh bien k c’est une fonction. Donc on va dire u(x) = k, ok ? Donc on sais dériver u(x). La dérivée d’une constante c’est zéro.
De la même façon, je vais garder f, bon je vais l’appeler v parce que c’est plus classique. v c’est f(x), et donc v'(x) c’est f'(x) simplement, d’accord ?
Donc ici, la fonction de départ, eh bien elle de la forme u * v et on connaît sa dérivée. La dérivée de u * v c’est u’v + uv’. Si vraiment t’as envie de te compliquer la vie : u’ c’est zéro, ça tombe bien.
Autrement dit, ça va être égal à 0*v + u c’est k * v’. Donc tu as bien k * v’ et v’ c’est f(x). Ça tombe bien, ça fait k * f'(x) !
La dérivée de k * f(x) c’est donc bien k * f'(x). Si tu as envie de te compliquer la vie, tu peux passer par là, mais c’est beaucoup plus simple de te rappeler simplement que quand tu multiplies une fonction, sa dérivée, elle est multipliée par le même facteur.
Voilà comment tu peux trouver la dérivée de la fonction k * f(x) !
Clique ici pour voir plus de vidéos sur ce thème, et abonne-toi à la chaine Youtube.