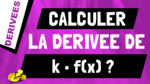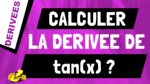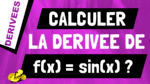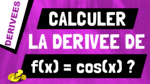Dans cette vidéo, je vais te montrer comment retrouver et calculer la dérivée d’une composition de fonctions.
Déjà une composition de fonctions, c’est simplement au lieu de prendre f(x), on va prendre f d’une fonction. Par exemple f(g(x)) et on veut dériver cette formule. Alors qu’est ce qu’on obtient ? On obtient f'(g(x)) * g'(x). Alors
Comment se rappeler de la formule de la dérivée d’une composition de fonctions ?
Déjà, on peut faire l’analogie avec f(x). Quand on dérive f(x), d’accord ici si on dérive, on obtient f'(x). Maintenant qu’est-ce qui change ? Ici on a f mais on n’a pas x, on a g(x), donc quand on va dériver, il va se passer des choses différentes.
La première chose c’est on va garder la même forme, c’est à dire on va avoir f'(g(x)). Ici, on a simplement remplacé x par g(x), ça c’est la première partie de la dérivée.
Mais comme ici on a g(x) et pas juste x, et bien il va se passer quelque chose d’autre. C’est qu’on va multiplier par g'(x) ! On va multiplier par la dérivée de la fonction qui est à l’intérieur des parenthèses de f.
Et c’est ça la seule chose qui est à savoir en fait. Si tu sais dériver f, tu vois que tu sais dériver g, tu vas utiliser g(x) et le tout tu vas le multiplier par g'(x). Si tu sais faire, tu sais trouver la dérivée la composition de fonctions f(g(x)).
Au final, la dérivée de f(g(x)), c’est simplement f'(g(x))… c’est le truc complètement naturel… et puis tu viens rajouter ici quelque chose d’important c’est la multiplication par g'(x) !
Un exemple pour bien comprendre.
Si on prend un exemple ici quand on veut dériver par exemple (√ x)^7. Donc qu’est ce qu’on a ici ? Quelles sont les deux fonctions ?
On voit qu’on a une fonction exposant 7 et une fonction racines de x. Alors laquelle est laquelle ? Et bien on voit qu’ici c’est √x qui est à l’exposant 7. Ce qui veut dire qu’on a appliqué l’exposant 7 à √x.
Donc la formule ici on aurait une première fonction qui est x^7 et une autre qui est √x. Alors tu vois qu’ici on n’a pas x^7 dans notre fonction, on a (√x)^7.
Autrement dit, cette fonction là ça va être f(x). Et celle ci ça va être g(x). Donc ça c’est la dérivée, g'(x) c’est 1/2√x, et f'(x) et bien on sait dériver ça aussi, c’est 7 x^6.
À partir de là, on a bien notre formule ici et on veut simplement appliquer les choses. Donc on a dit on a f c’est x^7, donc quand on va dériver on va pas avoir juste 7 x^6, mais on va avoir 7 * √ x^6. Ici on va avoir 7 * √ x^6.
Tu vois que c’est simplement la dérivée de la fonction qu’on a dehors, et à la place de x, on a mit √ x. Puis on va multiplier par la dérivée de ce qu’on a à l’intérieur. 1/2√x.
Voilà donc là on pourrait, on pourrait simplifier un peu tout ça puisque √ x^6 c’est x^3 divisé par 2√ x, voilà. Pas besoin d’aller plus loin.
Résumé :
Ce qui est important ici c’est ce passage ici ! Tu vois qu’ici on va utiliser la dérivée de la fonction qui englobe tout ça, et on a juste remplacé √x. Ensuite on vient multiplier par la dérivée de √ x. D’accord?
La seule chose à retenir c’est que ça marche pareil c’est à dire que de f(x) on passe à f’. Et de f(g(x)), on va passer la f'(g(x)) et après on multiplie par g'(x).
Clique ici pour voir plus de vidéos sur ce thème, et abonne-toi à la chaine Youtube.